课程名称 |
高级语言程序设计(上) |
授课对象所属专业 |
物联网工程 |
课程类型 |
专业教育 |
开课年级 |
2023级 |
课程性质 |
专业课 |
课程总学时 |
42 |
一�、课程简介(300字左右)
《高级语言程序设计(上)》是高等院校物联网工程专业学生的一门基础专业课程����,课程以C语言为教授程序设计的描述语言,结合语言介绍程序设计的基本原理�、技巧和方法。本课程主要包括以下内容:程序设计基本概念、基本数据类型���、运算符与表达式����、数据输入输出函数��、基本语句结构(顺序结构程序设计�����、选择结构程序设计和循环结构程序设计)�、函数以及编译预处理等。本课程旨在培养学生具有设计计算机程序���、编写程序和调试程序的能力�����。同时����,为后续在嵌入式平台进行交叉编译以及程序开发打下扎实的基础�。
课程坚持立德树人的教育之本,针对课程构建具有思政育人的理论与实践教学�,将思政元素融入教学各个环节。通过教学案例�,鼓励学生透过知识和内容,挖掘蕴含在知识背后的思维方式�、价值观和文化意义。培养学生的科学素养����,强化学生的创新意识,提高学生的创新能力��。培养学生树立和践行社会主义核心价值观����,增强责任意识,鲜明政治取向��,促使学生成长成才��,并最终实现知识传授与价值引领相结合的育人目标��。
二�、案例基本信息
1.案例名称:从历史的辉煌到今天的奋发图强——杨辉三角
2.对应章节:第五章第6节
3.课程讲次:2课时
三、案例教学目标
目标:通过对杨辉三角起源认知�����,把循环结构概述、while语句���、do-while语句�、for语句以及循环的嵌套的理解及应用融入其中��,从历史角度激发学生的爱国热情和民族自豪感���,同时也让学生树立坚定的信念���,严谨的科学态度,开拓的创新精神��,向科学家学习�����,成长为思想政治可靠�、专业技术优秀的建设人才。
重点:while�、do-while和for语句的应用。
难点:循环的嵌套��。
四、案例主要内容
1.利用杨辉三角理解goto语句以及用goto语句构成循环�。
2.利用杨辉三角熟练掌握while、do-while以及for语句���。
3.利用杨辉三角掌握循环嵌套的应用。
4.通过杨辉三角使学生知道杨辉及中国在世界数学界的历史成就���,激发学生的爱国热情和民族自豪感�����,向科学家学习严谨的科学态度和开拓的创新精神��。
五���、案例教学设计
1、历史引入:从南宋杰出数学家杨辉所著的《详解九章算法》出发���。
杨辉��,字谦光�����,南宋时期杭州人��。在他1261年所著的《详解九章算法》一书中��,辑录了三角形数表�����,称之为“开方作法本源”图���。历史上曾经独立绘制过这种图表的数学家有:贾宪 中国北宋11世纪 《释锁算术》����。杨辉 中国南宋1261《详解九章算法》记载之功���。朱世杰 中国元代1299《四元玉鉴》级数求和公式���。阿尔·卡西 阿拉伯1427《算术的钥匙》。阿皮亚纳斯 德国1527����。米歇尔.斯蒂费尔 德国1544《综合算术》二项式展开式系数。薛贝尔 法国1545����。B·帕斯卡 法国1654《论算术三角形》���。
2、历史故事与三角样式:探究杨辉三角的历史故事和三角样式����,分析模型特点�,确定数组结构。
三角形数表最早引自11世纪中叶(约公元1050年)贾宪的《释锁算术》����,并绘画了“古法七乘方图”。故此�,杨辉三角又被称为“贾宪三角”。元朝数学家朱世杰在《四元玉鉴》(1303年)扩充了“贾宪三角”成“古法七乘方图”�����。意大利人称之为“塔塔利亚三角形”(Triangolo di Tartaglia)以纪念在16世纪发现一元三次方程解的塔塔利亚�����。在欧洲直到1623年以后�,法国数学家帕斯卡在31岁时发现了“帕斯卡三角”����。布莱士·帕斯卡的著作Traité du triangle arithmétique(1655年)介绍了这个三角形�����。帕斯卡搜集了几个关于它的结果����,并以此解决一些概率论上的问题,影响面广泛���,Pierre Raymond de Montmort(1708年)和亚伯拉罕·棣·美弗(1730年)都用帕斯卡来称呼这个三角形�����。21世纪以来国外也逐渐承认这项成果属于中国��,所以有些书上称这是“中国三角形”(Chinese triangle)��。
中国古代数学家在数学的许多重要领域中处于遥遥领先的地位���。中国古代数学史曾经有自己光辉灿烂的篇章,而杨辉三角的发现就是十分精彩的一页。
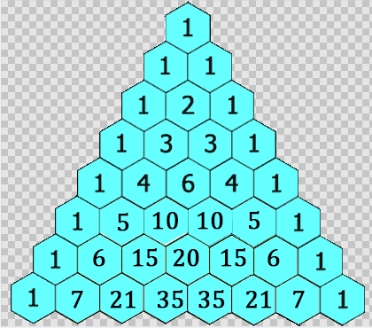
下面讲解三角样式及模型:
每个数等于它上方两数之和����。
每行数字左右对称,由1开始逐渐变大�����。
第n行的数字有n项�。
前n行共[(1+n)n]/2个数。
第n行的m个数可表示为C(n-1�����,m-1)��,即为从n-1个不同元素中取m-1个元素的组合数�����。
第n行的第m个数和第n-m+1个数相等 �,为组合数性质之一���。
每个数字等于上一行的左右两个数字之和�����?���?捎么诵灾市闯稣鲅罨匀恰<吹趎+1行的第i个数等于第n行的第i-1个数和第i个数之和����,这也是组合数的性质之一。即C(n+1,i)=C(n,i)+C(n,i-1)����。
(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
将第2n+1行第1个数����,跟第2n+2行第3个数、第2n+3行第5个数……连成一线��,这些数的和是第4n+1个斐波那契数�����;将第2n行第2个数(n>1)�,跟第2n-1行第4个数����、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数�����。
将第n行的数字分别乘以10^(m-1)��,其中m为该数所在的列�����,再将各项相加的和为11^(n-1)��。11^0=1����,11^1=1x10^0+1×10^1=11����,11^2=1×10^0+2x10^1+1x10^2=121,11^3=1x10^0+3×10^1+3x10^2+1x10^3=1331�����,11^4=1x10^0+4x10^1+6x10^2+4x10^3+1x10^4=14641,11^5=1x10^0+5x10^1+10x10^2+10x10^3+5x10^4+1×10^5=161051����。
第n行数字的和为2^(n-1)。1=2^(1-1)���,1+1=2^(2-1)�����,1+2+1=2^(3-1)�����,1+3+3+1=2^(4-1)��,1+4+6+4+1=2^(5-1)����,1+5+10+10+5+1=2^(6-1)�。
斜线上数字的和等于其向左(从左上方到右下方的斜线)或向右拐弯(从右上方到左下方的斜线),拐角上的数字����。1+1=2��,1+1+1=3�����,1+1+1+1=4����,1+2=3�,1+2+3=6,1+2+3+4=10��,1+3=4��,1+3+6=10���,1+4=5����。
将各行数字左对齐����,其右上到左下对角线数字的和等于斐波那契数列的数字��。1,1�,1+1=2,2+1=3���,1+3+1=5����,3+4+1=8�����,1+6+5+1=13�����,4+10+6+1=21�����,1+10+15+7+1=34���,5+20+21+8+1=55�。
3����、递推规律:由模型特点发现递推规律�,确定推演公式��,核心代码生成���。
以下的代码均用标准C语言写成��,可以被包括MSVC(含VC6)�����、GCC的多种C编译器编译���。
(1)实现方式一
这个算法使用只行列位置和左侧的数值算出数值:
/* yh-rt1.c -时间和空间最优算法*/
#include <stdio.h>
#include <stdlib.h>
int main()
{
int s = 1, h; //数值和高度
int i, j; //循环计数
scanf("%d", &h); //输入层数
printf("1\n"); //输出第一个1
for (i = 2; i <= h; s = 1, i++) //行数i从2到层高
{ printf("1 "); //第一个1
for (j = 1; j <= i - 2; j++) //列位置j绕过第一个直接开始循环
//printf("%d ", (s = (i - j) / j * s));
printf("%d ", (s = (i - j) * s / j));
printf("1\n"); //最后一个1,换行
}
getchar(); //暂停等待
return 0;}
默认求直角三角形���,可通过注释的开关或使用编译器的-D定义开关调节等腰三角形和菱形输出����。如果觉得复杂��,可按照define使用的情况剔除因不符合ifdef条件从而未启用的代码之后阅读。
(2)实现方式二
这个算法创建了一个二维数组����,并且通过上一行的数值求当前行����。在反过来再次打印时,这个程序会使用以前算好的值�,从而节省了重复迭代的时间。
/* yh-2d.c -二维数组迭代*/
#include<stdio.h>
#define M 10 //行数
// #define PYRAMID //金字塔���,会额外填充空格
// #define REVERSE //反向再来一次���,得到菱形
int main(void)
{
int a [M][M], i, j; //二维数组和循环变量,a[行][列]
for (i = 0; i<M; i++) //每一行
{
#ifdef PYRAMID
for (j = 0;j <= M-i; j++) printf (" ");
#endif //填充结束
for (j = 0; j <= i; j++) //赋值打印
printf("%4d", (a[i][j] = (i == j || j == 0) ? 1 : //首尾置1
a[i - 1][j] + a[i - 1][j - 1] )); //使用上一行计算
printf("\n");
}
#ifdef REVERSE
for(i = M-2; i >= 0; i--)
{
#ifdef PYRAMID
for (j = 0;j <= M - i; j++) printf(" ");
#endif //填充结束
for (j = 0;j <= i; j++) printf("%4d",a[i][j]); //直接使用以前求得的值
printf("\n");
}
#endif //菱形结束
getchar(); //暂停等待
}
(3)实现方式三
这一个使用大数组写成����,风格更接近教科书上的VC6代码。
/* yh-rt3.c -较为暴力的大数组*/
#include <stdio.h>
#include "string.h"
int main()
{ int a[10000]; //容器����,由n*(n+1)/2<=10000可知,n<=141
int b,CR,i; //b为当前行数�,CR为要求显示的行数,i为循环数
printf("请输入要显示的行数(3~141):");
scanf("%d",&CR);
YHSJ(CR);
a[1]=a[2]=1; //前两行数值少且全为1���,故直接输出
printf("%d\n",a[1]);
printf("%d %d\n",a[1],a[2]);
for(b=3;b<=CR;b++) //从第三行开始判断
{ for(i=b;i>=2;i--) //从倒数第一个数开始加
a[i]=a[i]+a[i-1]; //杨辉三角的规律���,没有值的数组默认为0
for(i=1;i<=b;i++) //显示循环
printf("%d ",a[i]);
printf("\n"); //换行
}
return 0;}
六��、教学反思
通过这次课的讲解����,使学生知道杨辉是中国宋代著名的数学家�����,他整理杨辉三角领先于法国数学家帕斯卡近400年�,这是我国数学史上伟大的成就。通过对杨辉三角起源认知�����,激发学生的爱国热情和民族自豪感��,同时也让学生树立坚定的信念�,向科学家学习,成长为思想政治可靠����、专业技术优秀的建设人才�����。
通过学生参与和接受程度,不断更新课程思政教学内容�。教学过程的记录、行为学观察进行评价��、反馈�����,为后续教学保留宝贵教学经验��;通过表格量化考核����、学生撰写心得体会,并结合诊断性评价以及形成性评价的结果�����,给予学生定性或定量的评价��。
物联网工程教研室供稿
责编:魏东平 审稿:董西伟 刘妍
